エクセルで箱ひげ図を作成する方法
箱ひげ図は、データのばらつきや分布を一目で把握できる便利なグラフです。膨大な数値データを前に、全体像や傾向をつかむのが難しいと感じたことはありませんか？箱ひげ図を使えば、データの中央値や四分位範囲、外れ値まで直感的に確認することができ、分析作業が格段に効率化します。
特に、エクセルを活用すれば、数クリックで箱ひげ図を作成できるため、初心者の方でも簡単に取り組めます。本記事では、箱ひげ図の基本概念や具体的な作成手順を解説し、実務や日常のデータ分析で役立つ活用例もご紹介します。ぜひ参考にして、データ分析をさらに効果的に進めてみてください。
箱ひげ図とは
箱ひげ図は、データの広がり具合や分布を一目で確認できる視覚的な図表です。「箱」と「ひげ」の形で表現されるため、専門知識がなくても直感的に理解しやすい特徴があります。
箱ひげ図の見方
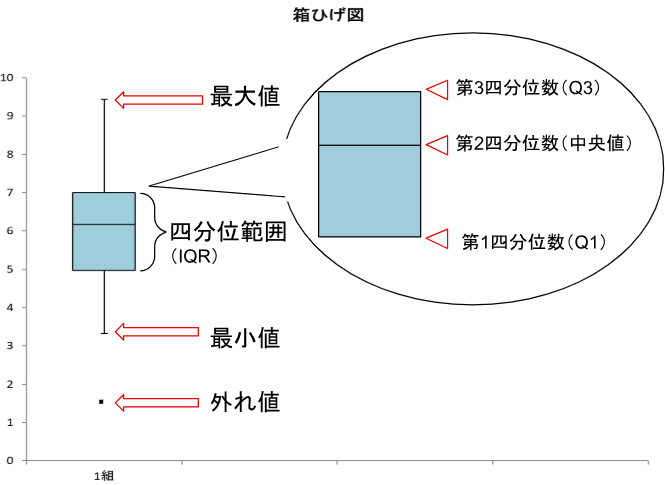
箱ひげ図は、次の要素で構成されています。
| パーツ名 | 説明 | 表示 |
|---|---|---|
| ボックス（箱） | データを小さい順に並べて4等分した際の区切り値である四分位数（Quartile）の範囲を示します。 | ・第1四分位数（Q1）：最小値から25%の値 ・第3四分位数（Q3）：最大値から25%の値 ・中央値：全データの中央の値 |
| ひげ（ウィスカー） | ボックスの上下に伸びる線で、データの全体的な範囲を示す。 | ・上のひげ：最大値（Maximum） ・下のひげ：最小値（Minimum） |
| 外れ値（アウトライヤー） | ボックスやひげの範囲外に位置する、他のデータから大きく離れた値。異常値や例外的なデータとして分析の手がかりとなる。 | ボックスやひげから離れた点で表示されます。 |
例えば、クラス全体のテスト点数を箱ひげ図で表すと、以下のような情報が一目で理解できます。
- クラスの平均的な点数の範囲
- 点数のばらつき具合
- 最高点数や最低点数、およびそれらが全体からどれほど離れているか
このように、箱ひげ図を使うことで、データの分布状況や中心的な傾向、ばらつきの度合い、分布の対称性など、多くの情報を視覚的に把握することができます。
箱ひげ図を使うことのメリット
箱ひげ図は、データの分布状況を視覚的に把握できる便利なツールであり、ビジネスや教育現場など幅広いシーンで活用されています。その特徴は、複雑なデータの特性を直感的に理解できる点にあります。以下に、具体的な活用場面とメリットを解説します。
- データの分布状況がひと目でわかる
数値データを羅列して見るだけでは把握しにくい全体像を、視覚的に理解できます。データがどの範囲に集中しているのか、どの程度ばらついているのかを直感的に把握できるほか、偏りや想定外の値も箱ひげ図の形状から読み取ることが可能です。 - 複数のデータセットの比較が簡単
異なる店舗の売上データや、複数クラスのテスト結果などを並べて表示することで、データごとの特徴や違いを視覚的に比較できます。数字だけでは気づきにくい傾向の違いも、箱ひげ図を使うことで明確になります。 - 異常値の検出が簡単
データ中の極端に高い値や低い値は、「ひげ」の先に点として表示されます。これにより、通常の範囲から外れた値（外れ値）を簡単に特定できます。たとえば、入力ミスの発見や、特別な注意が必要なデータを識別する際に役立ちます。 - データの対称性や偏りを把握できる
箱ひげ図の中央線の位置や「箱」と「ひげ」の長さの関係から、データが対称的か、特定の方向に偏っているかを判断できます。これにより、適切な分析手法を選択する際の重要な判断材料となります。
箱ひげ図は、複雑なデータの特性を視覚的に分かりやすく表現できる優れたツールとして、ビジネスや研究のさまざまな場面で活用されています。
箱ひげ図を使うことのデメリット
一方で、箱ひげ図には以下のようなデメリットも存在します。
- 分布の詳細な情報が分かりにくい
箱ひげ図はデータの大まかな分布を把握するのに適していますが、双峰性（二つの山を持つ分布）や多峰性（複数の山を持つ分布）など、詳細な分布形状の把握には不向きです。より正確な分析が必要な場合は、ヒストグラムや密度プロットと併用することが推奨されます。 - データ数が少ない場合の限界
データ数が少ない場合（一般的に30件未満）、箱ひげ図では情報量が不足し、誤った解釈を招く可能性があります。この場合、散布図などで個々のデータポイントを表示する方が適切です。 - 四分位数の計算方法による結果の違い
四分位数の計算には複数の手法があり、使用するソフトウェアや設定によって異なる結果が得られる場合があります。細かな分析が必要な場合は、どの計算方法が使用されたかを確認し、記録しておくことが重要です。
これらのデメリットを理解し、適切な場面で箱ひげ図を活用することで、その効果を最大限に引き出すことができるでしょう。
箱ひげ図の活用例
箱ひげ図は、さまざまな分野で活用されています。以下に、その具体的な例を挙げます。
- 教育分野
学生の試験結果の分布を分析することで、成績のばらつきや中央値、想定値を把握できます。これにより、教育方法の改善や個別指導の必要性を判断する材料となります。 - 医療分野
患者の検査結果や治療効果の分布を比較し、異常値を検出したり、治療法の効果を判定する際に活用されます。 - ビジネス分野
売上データや顧客満足度の分布を分析することで、業績評価やマーケティング戦略の策定に役立ちます。 - 製造業
製品の品質検査結果を確認し、不良品の検出や生産工程の改善に活用されます。
箱ひげ図の作成方法
エクセルを使えば、簡単に箱ひげ図を作成できます。ここでは、テストの成績をもとに、クラスごとの箱ひげ図を作成する方法を解説します。
1. データの準備
まず、箱ひげ図で表示するデータをエクセルシートに入力します。データは見やすさを考慮して、大きい順に並べ替えましょう。
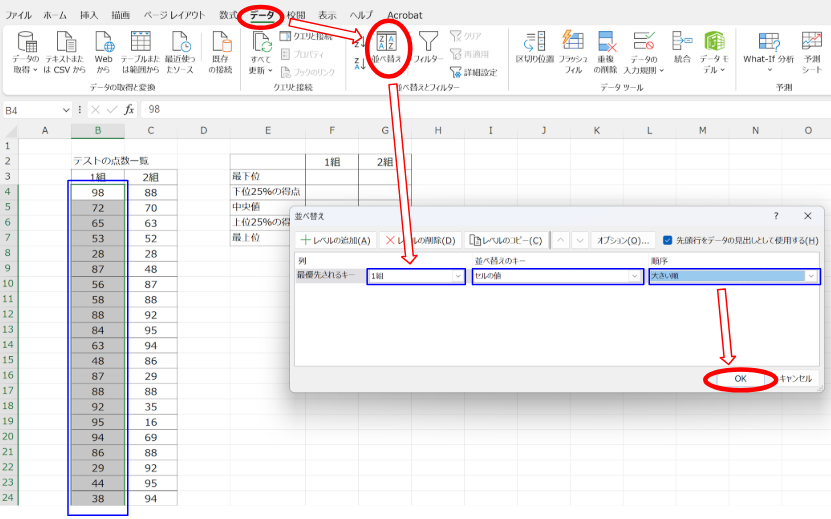
- データ範囲を選択し、「データ」タブの「並べ替え」をクリック。
- 並べ替え条件を「最優先されるキー: 1組」「並べ替えのキー: セルの値」「順序: 大きい順」に設定し、OKをクリックします。
2. グラフ化するためのデータ抽出
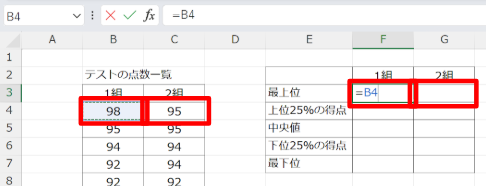
並べ替えたデータの一番上の値を「最上位」、一番下の値を「最下位」として別の欄に転記します。
3. 四分位数の計算
データの四分位数を計算するには、エクセルの QUARTILE.EXC 関数を使用します。
| QUARTILE.EXC＝（配列,戻り値） |
1組の得点リストがセル範囲「B4:B35」にある場合、上位25％の得点（第3四分位数）を求めるには、次の数式を入力します：
=QUARTILE.EXC(B4:B35, 3)
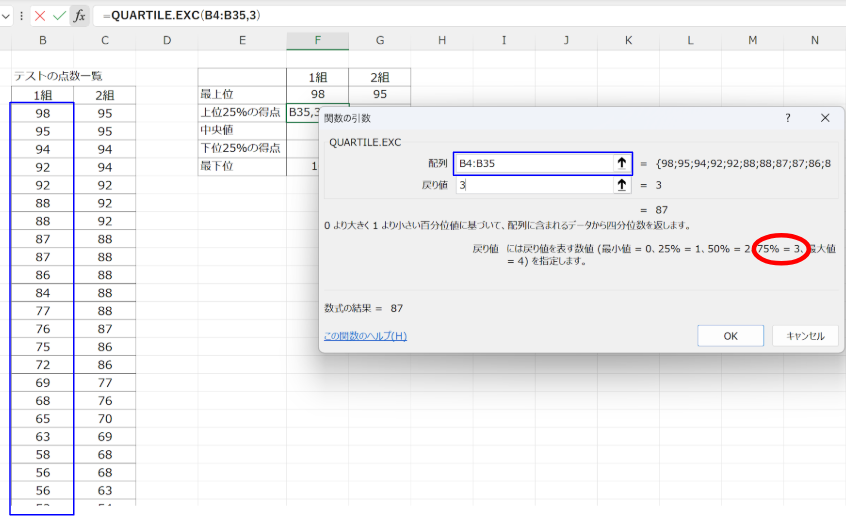
中央値や下位25％の得点も同様に、戻り値を変更して計算します：
- 第2四分位数（中央値）: 戻り値「2」
- 第1四分位数（下位25％）: 戻り値「1」
また、QUARTILE.INC 関数も利用可能です。両者の違いは、最小値と最大値の扱いにあります。
| QUARTILE.INC＝（配列,戻り値） |
QUARTILE.INC関数は、QUARTILE.EXC 関数と同じように使用しますが、最小値と最大値の扱いに違いがあるため計算方法が異なり、算出される数値に誤差が生じます。
| 関数 | 最小値と最大値の扱い |
|---|---|
| QUARTILE.EXC | 最小値と最大値を除外して計算。 |
| QUARTILE.INC | 最小値を0分位、最大値を1分位として含める。 |
目的に応じて使い分けてください。
4. 箱ひげ図の作成
四分位数などの数値が揃ったら、箱ひげ図を作成します。
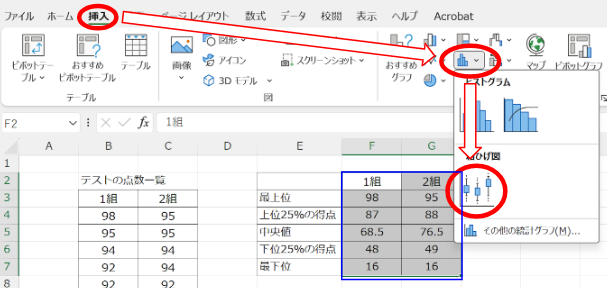
- データ範囲を選択します。
- 「挿入」タブをクリックし、「統計グラフの挿入」を選択します。
- 表示されるオプションから「箱ひげ図」を選択します。
5. 図のカスタマイズ
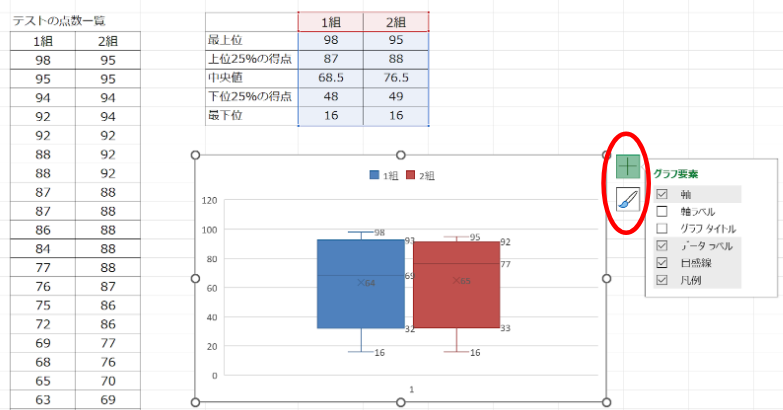
作成された箱ひげ図は、以下の方法でカスタマイズできます：
- グラフのタイトルや軸ラベルの編集: 図の右上にある「＋」アイコンをクリック。
- デザインやレイアウトの調整: 右上の筆マークをクリックし、好みに合わせて変更。
まとめ
箱ひげ図は、データの分布状況や中心傾向、ばらつき、異常値などを直感的に理解できる優れた図です。
教育、医療、ビジネス、製造業といった多岐にわたる分野で活用されており、複雑なデータの可視化に役立ちます。また、エクセルを使えば簡単に作成できるため、専門知識がなくても実践しやすい点も魅力です。一方で、分布の詳細な情報把握が難しい場合や、データ数が少ない場合の限界もあります。
これらの特徴を理解し、適切な場面で活用することで、箱ひげ図を効果的に使いこなすことができるでしょう。