相関係数とは?エクセルで相関係数を求める方法

エクセルを使ったデータ分析は、ビジネスや研究において欠かせないスキルの一つです。その中でも「相関係数」は、2つのデータの関連性を数値で表す便利な指標として広く活用されています。
たとえば、「広告費と売上の関係性」「気温と商品の売れ行き」「従業員の残業時間と生産性」など、ビジネスの現場では様々なデータの関連性を分析する機会があります。その際に最も基本的な手法が「相関係数分析」です。
本記事では、エクセルを使って簡単に相関係数を計算する方法を解説します。相関係数の基本から具体的な操作手順まで、わかりやすく説明していきますので、データ分析初心者の方でも安心して取り組んでいただけます。これを機に、データ間の関係性をしっかり把握して、より効果的な意思決定につなげましょう。
※ こちらの音声は、Google NotebookLM によって AI が生成したものです。そのため、発音や内容が正確でない場合があります。
相関分析とは

相関分析とは、二つのデータ間の関係性を探る手法です。
例えば、気温が高くなるとアイスクリームの売り上げも増える関係(正の相関)や、気温が低くなると温かい飲み物の売り上げが増える関係(負の相関)を見つけることができます。
また、相関が全く見られない場合は「相関がない」と言います。例えば、アイスクリームの売り上げと地震の発生頻度のように、全く関連性のないデータ間では相関は見られません。
相関関係と因果関係の違い
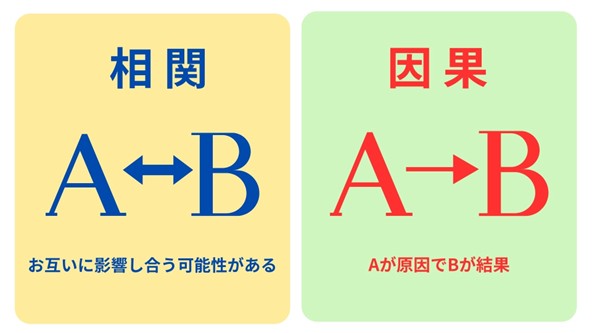
相関分析を行う際、多くの人が「相関関係」と「因果関係」を混同しがちです。
- 相関関係:二つのデータが互いに連動して変化することを指します。
例えば、蚊に刺された件数とアイスクリーム売上には相関関係がありますが、直接の因果関係はありません。両方とも夏という季節が原因ですが、蚊に刺されたからアイスクリームを食べたり、アイスクリームを食べたから蚊に刺されたりすることはありません。 - 因果関係とは、一方が原因となり他方に影響を及ぼす関係を指します。
例えば、雨が降ったために地面が濡れるというのは、原因と結果が明確な因果関係です。
このように、相関関係が存在するからといって因果関係があるとは限らない点を理解することが重要です。
相関分析と回帰分析の違い
相関分析と混同されがちな「回帰分析」も、データ分析の重要な手法です。両者の違いを簡単に見てみましょう。
- 相関分析:二つのデータ間の関連性を確認する手法です。
因果関係までは特定せず、関連性が強いか弱いかを数値(相関係数)で示します。 - 回帰分析:独立変数(説明変数)が従属変数(目的変数)にどのような影響を与えるかを分析します。さらに、一方のデータから他方を予測できるという特長があります。
たとえば、「Y = aX + b」のような数式を使い、予測モデルを構築することが可能です。
また、回帰分析は分析対象が二つの場合「単回帰分析」、複数の場合「重回帰分析」と呼ばれます。
相関分析が関連性を確認するための手法であるのに対し、回帰分析は予測や因果関係の強さを数値化するための手法です。
相関係数とは

2つの変数間の「相関関係の強さ」や「方向性」を数値で示す指標を相関係数と言います。この指標を活用することで、データ間の関連性を直感的に理解することが可能となります。特に「ピアソンの積率相関係数」は、最も一般的に使用される方法であり、変数同士の線形関係を評価する際に非常に有用です。

この計算により、変数間の関係性を正確に把握できます。
3種の相関
相関係数によって示される関係性は、主に以下の3つに分類されます:
- 正の相関
一方の変数が増加すると、もう一方の変数も増加する関係を指します。
例: 「学習時間」と「テストの点数」が高い正の相関を示す場合、学習時間が増えるほど、テストの点数も高くなる傾向があります。 - 負の相関
一方の変数が増加すると、もう一方の変数が減少する関係を指します。
例: 「通勤距離」と「通勤満足度」の間に負の相関がある場合、通勤距離が長くなるほど、満足度が低下することが分かります。 - 相関がない
2つの変数間に明確な関係性が見られない場合を指します。
例: 「靴のサイズ」と「年間読書量」の間に相関がない場合、どちらかの変数がもう一方に影響を及ぼす傾向は観察されません。
ピアソンの積率相関係数
ピアソンの積率相関係数は、変数間の線形関係を測定するための最も代表的な方法です。この指標は、-1から1の範囲をとり、値に応じて次のように解釈されます。
| 相関係数の値 | 相関性 |
|---|---|
| 0.8~1.0 (正の値) | 強い正の相関 |
| 0.3~0.7 (正の値) | 中程度の正の相関 |
| -0.2~0.2 | 相関がほとんどない |
| -0.3~-0.7 (負の値) | 中程度の負の相関 |
| -0.8~-1.0 (負の値) | 強い負の相関 |
※注意点
- 線形関係に限定: ピアソンの積率相関係数は、変数間の線形関係を測定します。非線形の関係が存在する場合、この指標は適切ではありません。
- 外れ値の影響: データセットに外れ値が含まれると、相関係数が歪む可能性があります。
- 因果関係の判断不可: 相関関係がある場合でも、それが因果関係を意味するわけではありません。
相関係数を求める方法

エクセルでは、相関係数を計算するためにCORREL関数やPEARSON関数を利用できます。これらの関数を使うと、データ間の相関関係を簡単に数値化でき、データ分析がより効率的になります。
CORREL関数を使う方法
CORREL関数 は、相関係数を計算する際に最もよく使われる関数です。以下に、実際の手順を示します。
| CORREL関数=(数値範囲1, 数値範囲2) |
使用例: 「学習時間」と「テストの点数」の相関係数を求めてみましょう。
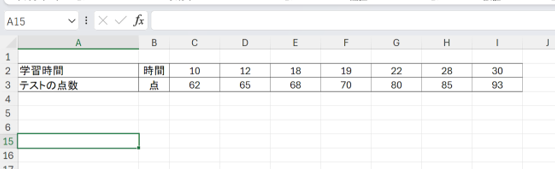
1.データを入力する
相関係数を算出したいデータを、それぞれ別の行に入力します。今回は「学習時間」を上の行、「テストの点数」を下の行に入力します。
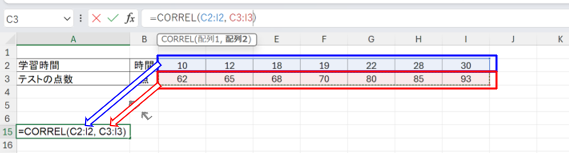
2. 相関係数を表示させたいセルを選択し、関数を入力する
選択したセルに次のように入力します:
=CORREL(C2:I2, C3:I3)
「C2:I2」は「学習時間」のデータ範囲、「C3:I3」は「テストの点数」のデータ範囲を指定しています。
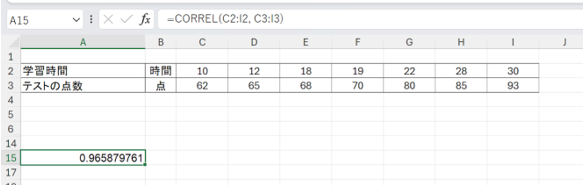
3.Enterキーを押す
計算結果として、指定したセル「A15」に相関係数が表示されました。
PEARSON関数を使う方法
PEARSON関数 もピアソンの相関係数を計算するための関数で、特徴としては古いエクセルバージョンとの互換性が高い点が挙げられます。基本的な使用方法はCORREL関数と同じですが、違いをあげるとすれば以下の3つが挙げられます。
- 計算方法がいくつか異なる
- 古いバージョンのエクセルとの互換性が高い
- 統計用語として一般的
| PEARSON関数=(数値範囲1, 数値範囲2) |
使用例: 「通勤距離」と「通勤満足度」の相関係数を求めてみましょう。
1.データを入力する
「通勤距離」のデータを上の行に、「通勤満足度」のデータを下の行に入力します。
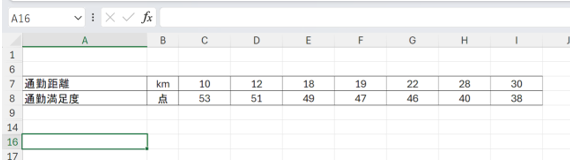
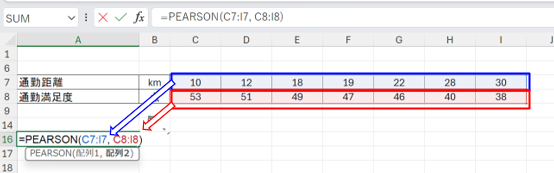
2. 相関係数を表示させたいセルを選択し、関数を入力する
選択したセルに次のように入力します:
=PEARSON(C7:I7, C8:I8)
「C7:I7」は「通勤距離」のデータ範囲、「C8:I8」は「通勤満足度」のデータ範囲を指定しています。
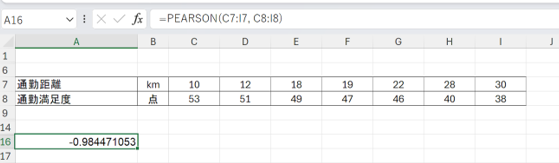
3.Enterキーを押す
計算結果として、指定したセル「A16」に相関係数が表示されました。
相関係数の活用シーン

相関係数は、データ間の関係性を数値で表す指標として、多くの分野で幅広く活用されています。ただし、数値だけに頼るのではなく、データの背景や方向性を考慮して活用することが重要です。以下では、具体的な活用シーンを分野別に紹介します。
1. マーケティングでの活用
マーケティングでは、広告費と売上、またはSNSエンゲージメントと新規顧客数などの関係性を分析する際に相関係数が役立ちます。
例えば、広告キャンペーンの投資効果を測定し、次回の施策計画を立てるための根拠を得ることが可能です。
2. 教育分野の活用
教育現場では、生徒の学習時間とテストの成績との相関を調べることで、成績向上のために有効な勉強時間や方法を導き出すことができます。
たとえば、「一定時間以上の学習を行うことで成績が向上する」などの結果を基に、学習指導の改善に役立てられます。
3. 健康管理での活用
健康分野では、運動時間と健康診断の結果の相関を分析することで、生活習慣の改善ポイントを見つけることが可能です。
例えば、運動時間と体重変化、または運動量と血圧との関係性を明らかにすることで、個人の健康管理計画に反映させることができます。
4. 製造業での活用
製造業では、生産条件(例: 温度や湿度)と製品の品質との相関を分析することで、品質向上のための改善ポイントを見つけ出すことができます。
たとえば、「湿度が一定値以上になると不良率が増加する」などの傾向を把握し、製造プロセスの最適化に役立てることが可能です。
5. 経済分析での活用
経済分析では、消費者支出と経済成長率の相関を調べることで、消費動向が経済全体に与える影響を分析できます。
この分析結果は経済予測や政策決定の指針となるので、消費の動向に合わせた戦略策定が可能になります。
まとめ
相関係数は、データ間の関係性を数値で示す指標として有用であり、マーケティングや教育、健康管理、製造業、経済分析など、さまざまな分野で幅広く活用されています。
ExcelのCORREL関数やPEARSON関数を使うことで、簡単に相関係数を計算し、データの関係性の強さや方向性を把握できます。
相関係数は因果関係を示すものではないので、データの背景を考慮して活用することが重要です。相関係数を正しく理解し、他の分析と組み合わせることで、より効果的な意思決定が可能になります。
